Created Wed May 22, 2024 at 9:07 PM

Lecture notes

Lecture #

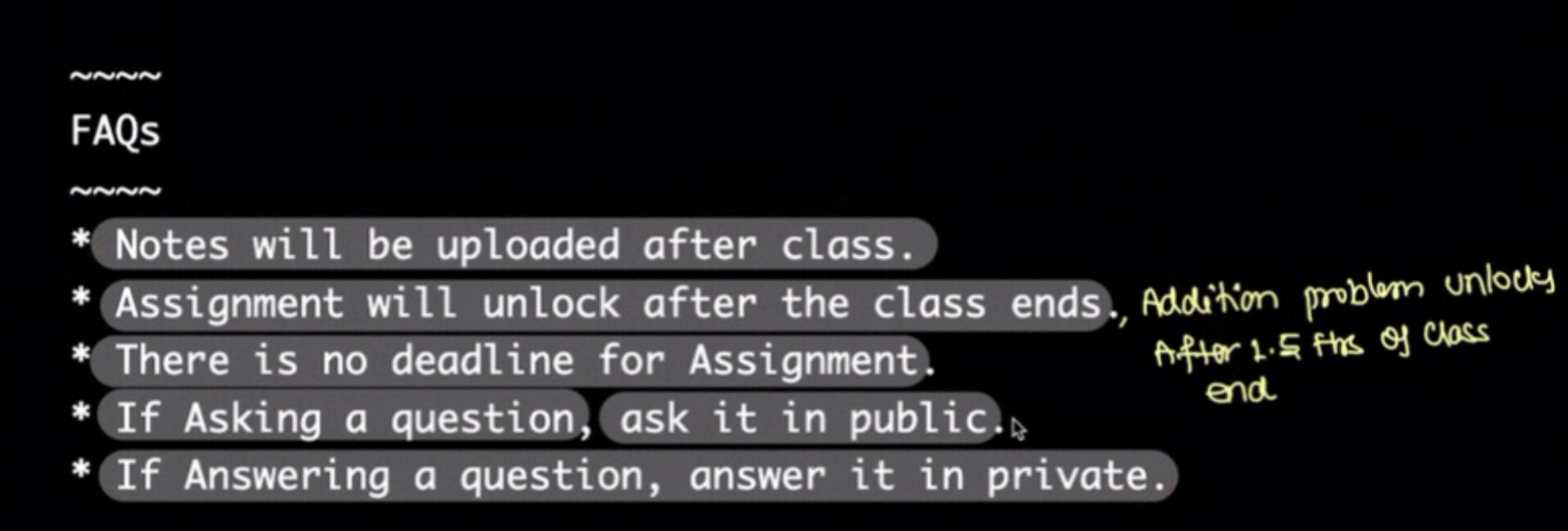
FAQs #

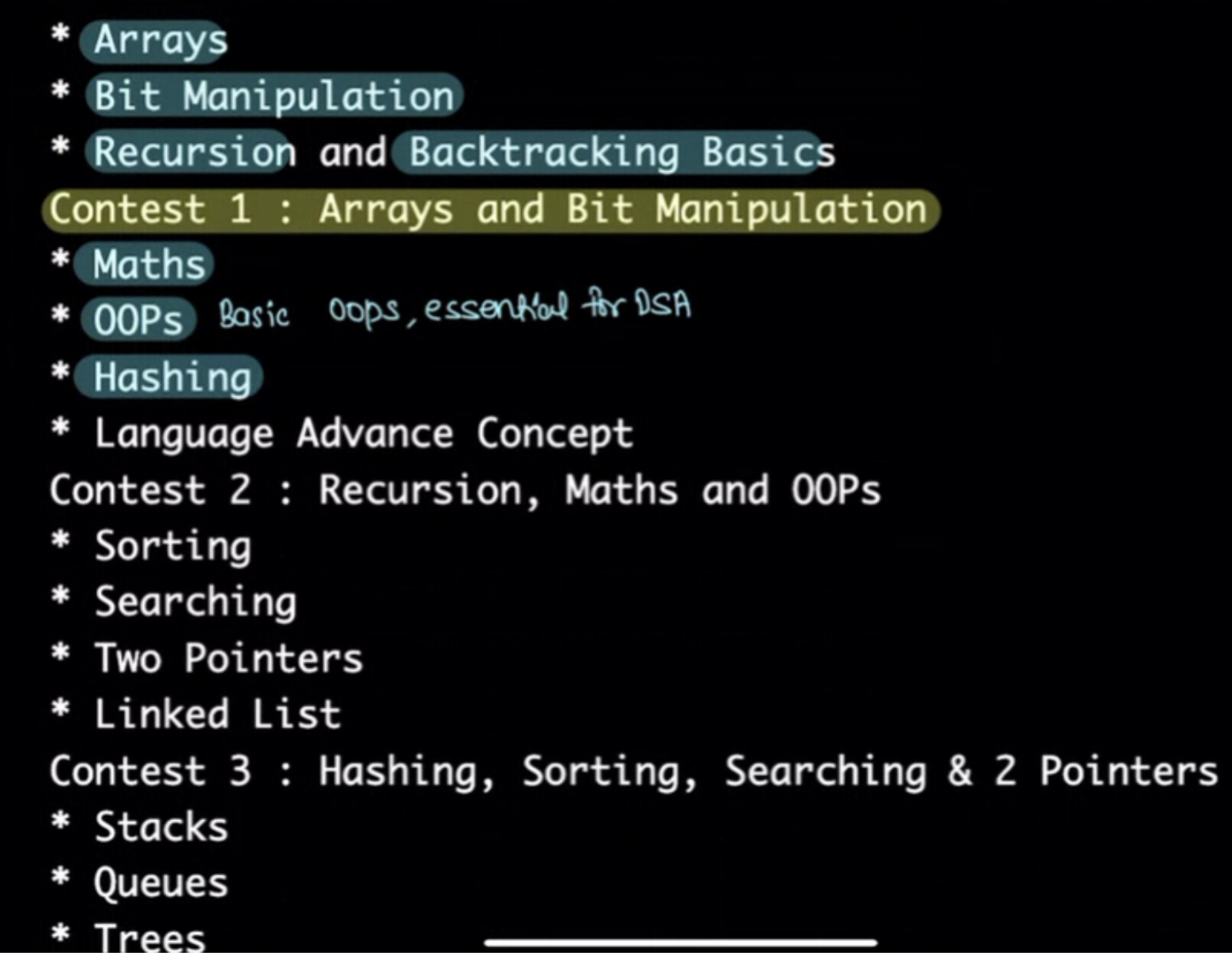
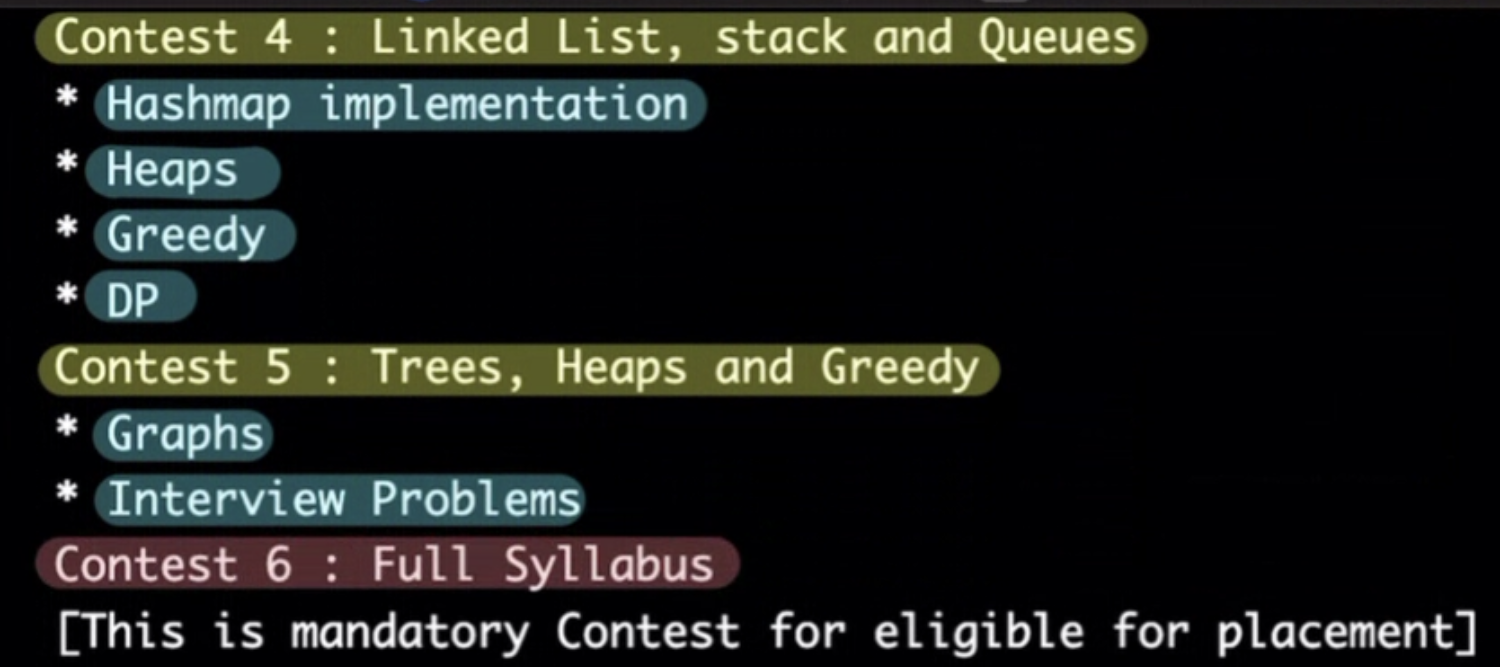
Focus of coming modules #

First quiz #

Q1: Sum of first n natural numbers. Q2: Range (count) between numbers. Inclusive: b-a+1, exclusive: b-a-1, one-side: b-a. Q3: Given N > 0, count number of factors. 1, 1, 2, 5, 10 algorithm for this, iterate (+1) until i*\i <= N Q4: Prime algo (skip) Q5: Nested loop table trick (make a table). Columns: i value, j value (… loops), count.

Big Oh #

1. Consider only the largest order term
2. Ignore multiplicative constants

Cases of TC #

Worst case, average case, best case.

Space complexity (input/output) #

Input and output space is not taken into account in space complexity. Only memory that’s used to solve the problem counts.

Example: Given some queries, storing answers in an array would not be counted in space complexity. We could just as well have printed it. i.e. it was a format requirement not the algorithm requirement.

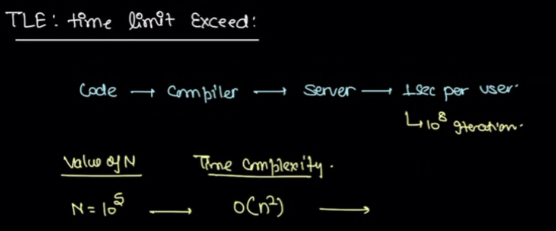
TLE (time limit exceeded) #

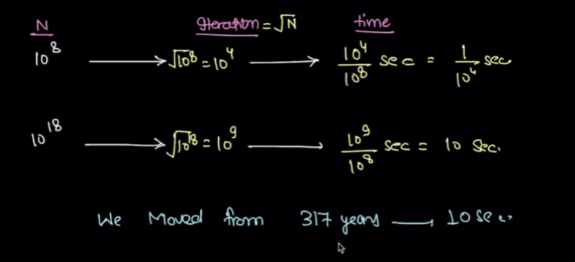
Assumption: Code judge provides only 1 sec for your program to run. If it exceeds that time, you’ll get TLE. Assumed processing time: 10^8/s.

Q: Any usual memory constraint, like10e8 assumption? A: usually no limit, but 10^4 size memory. And it usually comes for only in C++.

Bitwise operator works on bits of data #

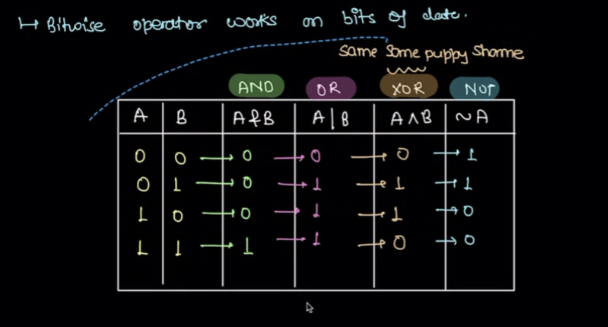
• a | b >= max(a, b)
• a & b < max(a, b)
• XOR: no relation
• ~a changes sign.
  • +ve, 0 become -ve
  • -ve become +ve, 0
• 1 left shift -> 2 * a.
  • If a = 1, then k left shift = 2^k. This means 2*n without loop is a single expression, (1 << n). In O(1) time complexity. Important optimization in coding
• 1 right shift -> floor(…floor(a/2)) or directly a/2^n. Actually the prior, but answer wise both are equivalent (since off by 1 is rounded off if number is int), so O(1).

Sq root of n #

• Takes time log(n) if we do binary search.

Summary #

Assignments #

• 10 basic time complexity questions, like given code’s complexity.

Code problem 1 #

Given an integer A, you need to find the count of it’s factors. Factor of a number is the number which divides it perfectly leaving no remainder. Example : 1, 2, 3, 6 are factors of 6

module.exports = { 
 //param A : integer
 //return an integer
	solve : function(A){
		A = BigInt(A);
		let i = BigInt(1);
		let j = BigInt(0);
		let count = BigInt(0);

		while(true) {
			if(A%i===BigInt(0)) 
			{
				j = A/i;
				if(i<j) {
					count+=BigInt(2);
				}
				else if(i===j) {
					count+=BigInt(1);
					break;
				}
				else
					break;
			}
			i+=BigInt(1);
		}
		return Number(count);
	}
};

Code problem 2 #

Write a function that takes an integer and returns the number of 1 bits present in its binary representation.

module.exports = { 
 //param A : integer
 //return an integer
	numSetBits : function(A){
        // A = BigInt(A);
        let count = 0;
        while(A) {
            if(A%2) count+=1;
            A = Math.floor(A/2);
        }
        return count;
	}
};