6. Bipartite Graph #
Created Monday 27 July 2020
When a graph can be divided into two parts such that all edges are between the two parts.
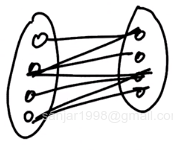Question: Given a graph, check whether it is bipartite or not?
- A useful property of a bipartite graph - A graph is bipartite iff it has no odd lengthed cycle.
Proof: A graph = tree with cycles. Trees are always bipartite. The only thing left are cycles. A cycle is never bipartite, so a graph with cycle is never bipartite. And a graph with no cycle(a tree) is always bipartite.
Algorithm:
- Do DFS and put vertices in a queue
- Put a vertex in set1, and try to put all it’s neigbours in set2.