tags:

• dnc

6. Convolution #

Created Tue Jul 30, 2024 at 12:30 AM

What is a convolution #

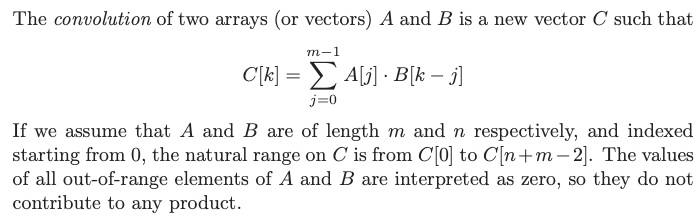Convolutions often arise when you are trying all possible ways of doing things that add up to k, for a large range of values of k, or when sliding a mask or pattern A over a sequence B and calculating at each position.

Speedup #

It turns out one can do convolution in nlogn instead of n² time. Kind of like sorting (squared to linearthmic)

Applications of convolution #

• Polynomial multiplication
• Integer multiplication faster than Karatsuba
• Cross-correlation - helps find out displacement between two time series A and B. Used in purchase vs advertising expenditure.
• Moving average filters - smoothing time series data by average over a window.
• String matching - not optimal but we can solve in nlgn. Need to binary encode characters however. Not the most efficient but showing that DnC works.
• Fast Polynomial Multiplication - Any polynomial can be represented as a set of points. Its easier to work with points, and DnC becomes applicable. We can do in nlgn instead of n²

Fast convolution solves many important problems in O(n log n). The first step is to recognize your problem is a convolution.